Hi there ![]()
I am computing a cluster-based permutation test in source space to identify significant correlations between dSPMs and rating differences in source space.
The issue is that I obtain 230 significant clusters from which the majority (approx. 80%-90%) consist of 1 vertex x 1 time-point, see Fig. below. I tried looking for solutions at the adjacency, but imo it looks like its properly defined.
Also varying the cluster-forming threshold does just result in less significant cluster but does strangely not change the size/length of the cluster (still mostly 1x1).
I would appreciate every hint or ideas to why that is the case or what I could try to solve it ![]()
Best,
Brais
I tried to create a MWE, though due to the random structure of the data it might not lead to the same results as I got. Also, the cluster-based permutation test is rather slow, probably due to the custom function using spearmanr:
import numpy as np
import mne
from scipy.stats import spearmanr
from mne.stats import spatio_temporal_cluster_test
import seaborn as sns
#Define some functions for the correlation
def critical_r_onesided(n, alpha = .05 ):
df = n - 2
critical_t = scipy.stats.t.ppf(1-alpha, df)
critical_r = np.sqrt( (critical_t**2) / ( (critical_t**2) + df ) )
return(critical_r)
def spearman_stat_fun(X, Y):
# 2D case: (n_subjects, n_features)
n_subjects, n_features = X.shape
correlations = np.zeros(n_features)
# Extract behavioral data
behavioral_data = Y[:, 0] if Y.ndim > 1 else Y
# Check if behavioral data has variance
if len(np.unique(behavioral_data)) <= 1:
return correlations
# Compute correlation for each feature
for feat in range(n_features):
eeg_data = X[:, feat]
if len(np.unique(eeg_data)) > 1:
correlation, _ = spearmanr(eeg_data, behavioral_data)
correlations[feat] = correlation if not np.isnan(correlation) else 0.0
return correlations
#generate random data
#source data
X_test = np.random.randn(33, 37, 5124) #subjects x timepoints x vertices
#behavioral data
Y_test = np.random.randn(33, 1) #1 rating per subject
#now transform the behavioral data to fit the shape of the source data
n_subjects = np.shape(X_test)[0]
n_times = np.shape(X_test)[1]
n_vertices = np.shape(X_test)[2]
Y_stc = np.zeros((n_subjects , n_times, n_vertices))
for subj in range(n_subjects):
# Fill all channels and timepoints with this subject's behavioral difference
Y_stc[subj, :, :] = Y_test[subj]
#get critical value for correlation test.
corr_thresh = critical_r_onesided(n_subjects, alpha=0.05) * -1
#define adjacency
fwdFP = <custom path to forward solution>
fwd = mne.read_forward_solution(fname = fwdFP)
fwd_adjacency = mne.spatial_src_adjacency(fwd["src"])
#<COOrdinate sparse array of dtype 'int64'
#with 35844 stored elements and shape (5124, 5124)>
test_src_obs, test_src_clusters, test_src_cluster_p_values, H0 = clu = spatio_temporal_cluster_test(
[X_test, Y_stc], # List of arrays to compare
stat_fun=spearman_stat_fun,
threshold=corr_thresh,
n_permutations=1000,
adjacency=fwd_adjacency,
n_jobs=-1,
tail=-1,
verbose=True)
#further investigate length/size of significant clusters
good_clusters_idx = np.where(test_src_cluster_p_values < 0.05)[0]
c_space = list()
c_time = list()
for c_idx in good_clusters_idx:
time_inds, space_inds = np.squeeze(clusters[c_idx])
c_time.append(len(np.atleast_1d(np.unique(time_inds))))
c_space.append(len(np.atleast_1d(space_inds)))
#visualization of cluster size
c_time.count(1) / len(c_time)
c_space.count(1) / len(c_space)
sns.kdeplot(np.array(c_space))
sns.kdeplot(np.array(c_time))
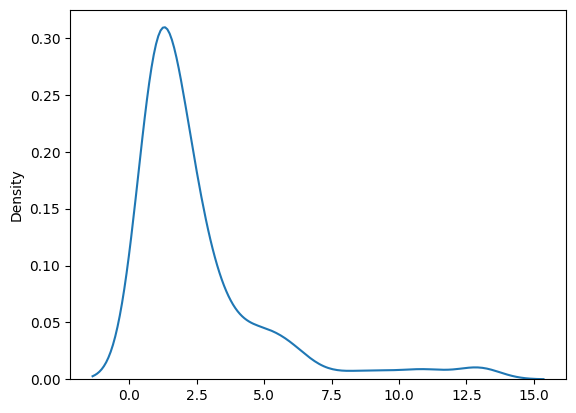
Density plots illustrating that the majority of clusters consist of 1 vertex/1 time-point:
No. of time-points:
No. of vertices:
Figure showing results of my cluster-based permutation test:
Note: colorbar gives temporal extent as obtained from
stc_all_cluster_vis = summarize_clusters_stc(
clu, subject="fsaverage",tstep = tstep, vertices=fsave_vertices, p_thresh = 0.05)